엘리스 AI 트랙 11주차 - 알고리즘을 위한 자료구조 (3/10) 🔥

✔ 11주차. 자료구조와 알고리즘

<학습 목표>

1. 개발역량 강화를 위한 자료구조 및 알고리즘 문제를 수행할 수 있습니다.
2. 알고리즘 문제를 만났을 때 효율적으로 접근하는 방법을 알 수 있습니다.
3. 알고리즘 문제 해결 기법의 근본적인 이해를 할 수 있습니다.

---

[01 자료구조와 알고리즘이란?]

1. 자료구조와 알고리즘
  - 프로그램의 기본 구성 : Input → Process (Store) → Output

https://www.tutorialspoint.com/software_engineering/software_analysis_design_tools.htm

2. 자료구조
  - 자료구조 : Data Structure. 데이터의 흐름과 저장.  정수, 실수, 문자, 배열, 해쉬 링크드리스트, 스택, 큐, 트리, 그래프 등등
  - 때와 장소에 맞는 자료구조가 필요하다.

3. 알고리즘
  - Algorithm. 주어진 문제를 어떻게 시간과 공간의 효율성을 고려해서 해결하면 좋을지에 대한 고민.
  - 좋은 알고리즘 : 적절한 입력, 적절한 출력, 명확성(어떤 수행을 위해 존재하는지 명확), 유효성(무한루프X), 효율성(효율성↑ 좋은 알고리즘)
  - 자료구조 → 알고리즘 : 자료구조를 활용해 어떤 문제를 해결
  - 알고리즘 → 자료구조 : 주어진 상황에 잘 맞는 자료구조를 구현하기 위해 알고리즘이 필요
✔ 자료구조와 알고리즘은 뗄레야 뗄 수 없는 관계

# 풀이 1
def maxTwoDiff(nums):
    nums.sort()
    # nums.sort() 시간복잡도 : O(NlogN)
    return nums[-1] - nums[0]

# 풀이 2
def maxTwoDiff(nums):
    # max,min 시간 복잡도 : O(N)
    return max(nums) - min(nums)

def main():
    print(maxTwoDiff([2, 8, 19, 37, 4, 5, 12, 50, 1, 34, 23])) # 가장 큰 두 수의 차

4. 객체
  - 객체 : 상태(속성, State, Property)와 행동(Behavior, Method)을 가지는 모든 것.
  - ex. 차의 상태 (색상, 모델 등), 차의 행동 (가속, 정지 등)
  - 객체지향 프로그래밍(OOP, Object Oriented Programming) ↔ 절차지향 프로그래밍
# 객체지향 프로그래밍하고 절차지향 프로그래밍이 반대인가? 반대는 아닌 것 같은데... 두개의 차이는 있겠지만 그게 반대의 의미로 쓰이지는 않을 것 같음. 적어도 내가 써보고 느끼기엔. 이거에 대해서는 좀 더 생각해 볼 것.
  - 객체지향 프로그래밍의 특징
    ① 캡슐화 : 코드를 묶어서 저일, 정보 은닉
    ② 상속 : 기존코드 재활용
    ③ 다형성 : 코드를 더 간단하게

[02 효율적인 프로그램이란?]

1. 시간/공간 복잡도
  - 효율성의 측정 방식 : 시간 복잡도, 공간 복잡도
  - 시간 복잡도 : 코드가 얼마나 빠르게 작동하는가. ↑ 코드 느려짐. 알고리즘에 사용되는 총 연산 횟수(실행시간 아니고 연산횟수임).
  - 공간 복잡도 : 코드가 얼마나 많은 메모리를 사용하는가. ↑ 메모리 많이 사용. 알고리즘에 사용되는 메모리 공간의 총량
✔알고리즘에서는 시간복잡도를 많이 따짐
  - 시간 복잡도 맛보기

sum = 0  # 연산 1번
for i in [1, 2, 3, 4]:
	sum += i;  # 연산 총 4번 => 시간 복잡도 5회

###

def doNothing(nums):
    return nums  # 연산 1번 => 시간 복잡도 1회

  - Big-O : 시간복잡도 함수의 가장 높은 차수(계수는 고려X, 시간 복잡도에 미치는 영향이 미미함)  # 차수란?

def doNothing(nums):
    return nums  # 시간 복잡도 1회 == Big-O 시간 복잡도 O(1)

  - 복잡도의 중요성 : N의 크기에 따라 기하급수적으로 증가함

https://www.bigocheatsheet.com/

  - Big-O 시간 복잡도 계산

# For / while loop가 한 번 중첩될 때마다 O(N)
for num in nums:  # O(N)

for i in range(len(nums)):
    for j in range(len(nums)):    # O(N^2)

for i in range(len(nums)):
    for j in range(len(nums)):
        for k in range(len(nums)):    # O(N^3)


# 자료구조 사용, 다른 함수 호출에는 각각의 O(N)을 파악
nums = [2, 8, 19, 37, 4, 5]
if num in nums:    # O(N)

nums = {2, 8, 19, 37, 4, 5}
if num in nums:    # O(1)

nums.sort()    # O(NlogN)


# 매번 절반씩 입력값이 줄어들면 O(logN)

  - Big-O 공간 복잡도 계산

a = 1    # 공간 복잡도 O(1)

a = [num for num in nums]    # 공간 복잡도 O(N)

a = [[num for num in nums] for num in nums]    # 공간 복잡도 O(N^2)

2. 배열
  - 배열 : 가장 기본적인 자료 구조. 공간 복잡도 = O(N)
  - 배열의 시간 복잡도

# 인덱스 알 때
nums = [1, 2, 3, 4, 5, 6]
nums[2]    # O(1)

# 인덱스 모를 때 하나씩 검사
if 5 in nums:    # O(N)

# 배열 전부 순회
for num in nums:    # O(N)

# 자료 끝에 추가
nums.append(7)    # O(1)

# 자료 중간에 추가
nums.insert(3, 9)    # O(N)

  - 문자열 : 문자들의 배열(배열의 한 종류임)
  - 2차원 배열 : [[1,2,3,4], [5,6,7,8]]

3. 해쉬
  - Hash : Key에 Value를 저장하는 자료구조. Key는 중복될 수 없으며 공간 복잡도는 대략 O(N)
  - 해쉬 Big-O 시간 복잡도

studentIds = { "박지나" : 123, "송호준" : 145, "이주원" : 563 }

# Key를 이용해서 Value 가져오기
print(studentIds["박지나"])    # 대략 O(1)

# Key가 존재하는지 확인하기
if("박지나" in studentIds):    # 대략 O(1)

# Key, Value 추가하기
studentIds["손지윤"] = 938    # 대략 O(1)

# 해당 Key의 Value 변경하기
studentIds["박지나"] = 555    # 대략 O(1)

  - 해쉬 공간 복잡도 : O(N). 데이터 없이 여유공간 많아야 성능유지
  - Set : Value 없이 Key만 있는 Dictionary

4. 배열과 해쉬의 trade-off
  - 해쉬 : 식별자가 있는 데이터, 시간 복잡도↓ / 공간 복잡도↑
  - 배열 : 식별자가 없는 데이터, 시간 복잡도↑ / 공간 복잡도↓

[03 심화된 자료구조]

1. 연결 리스트
  - 연결 리스트 : Linked List. 여러개의 노드들이 한 줄로 연결 (노드 = 저장할 데이터 + 다음 노드로의 연결)
  - 단순 연결 리스트 : 한 방향

https://www.geeksforgeeks.org/data-structures/linked-list/#singlyLinkedList

  - 이중 연결 리스트 : 양쪽 방향 (꼭 한 데이터를 가르키지 않아도 됨)

https://www.geeksforgeeks.org/difference-between-singly-linked-list-and-doubly-linked-list/

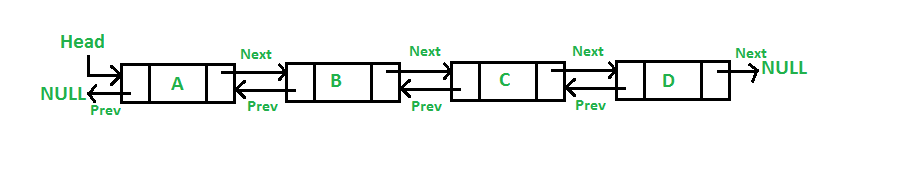
  - 원형 연결 리스트 : 맨 뒤 노드와 맨 앞 노드 연결

https://www.geeksforgeeks.org/circular-linked-list/

  - 기타 연결 리스트 : 아무형태나 가능

https://www.geeksforgeeks.org/skip-list/

  - 배열과 연결 리스트 차이 : 배열은 인덱스 이용, 연결 리스트는 현재 노드에서 연결된 노드로만 가능
  - 헤드 : Head. 연결리스트에서는 가장 처음이 무엇인지 정의 해줘야 함. 시작 노드를 뜻함.
  - 연결 리스트 시간 복잡도 : 자료 중간에 추가 or 삭제는 O(1) (배열보다 효율적)

2. 큐
  - Queue : FIFO (First In First Out)

https://dev.to/rinsama77/data-structure-stack-and-queue-4ecd

  - 큐 시간 복잡도 : 입출력 모두 O(1)
  - Queue In Python

# queue library 활용
import queue

q = queue.Queue()
q.put(2)
q.put(8)
q.get()  # 2

# 배열을 Queue 로 활용
q = [1, 2, 3, 4, 5]
q.insert(0, 6)  # [6, 1, 2, 3, 4, 5]
q.pop()  # [6, 1, 2, 3, 4]

3. 스택
  - Stack : LIFO (Last In First Out)

https://dev.to/rinsama77/data-structure-stack-and-queue-4ecd

  - 스택 시간 복잡도 : 입출력 모두 O(1)
  - Stack In Python

# 배열을 스택으로 활용
Stack = []
Stack.append(2)
Stack.append(5)
Stack.pop()  # 5

[04 자료구조의 끝판왕]

1. 재귀 함수
  - 프로그램의 핵심은 되풀이
  - 재귀 함수 : 스스로를 호출하는 방식의 반복법. 끝나야 하기 때문에 종료 조건이 필요함.
  - 팩토리얼 계산하기

# 반복
def iterationFactorial(num):
    x = 1
    for each in range(1, num + 1):
        x = x * each
    return x

# 재귀
def recursionFactorial(num):
    if num == 0:
        return 1
    return num * recursionFactorial(num-1)

2. 동적 프로그래밍
  - 동적 프로그래밍 : Dynamic Programming. 재귀 + 정보저장. 한 부분 문제를 한 번 계산했다면, 다시 계산할 필요가 없도록 저장값을 다른 자료구조에 저장
  - 피보나치의 수

class Fib():
    def __init__(self):
        self.memo = {}

    def fibonacci(self, num):
        if num == 0:
            return 0
        
        if num == 1:
            return 1
        
        if num in self.memo:
            return self.memo[num]
        
        self.memo[num] = self.fibonacci(num-1) + self.fibonacci(num-2)
        
        return self.memo[num]

3. 트리
  - 트리 : 나무 형태의 자료구조

http://www.btechsmartclass.com/data_structures/tree-terminology.html

  - 부모와 자식 : 부모 노드 à 자식 노드 방향으로 연결이 존재

http://www.btechsmartclass.com/data_structures/tree-terminology.html

http://www.btechsmartclass.com/data_structures/tree-terminology.html

  - 루트와 리프 : 루트는 부모X, 리프는 자식X

http://www.btechsmartclass.com/data_structures/tree-terminology.html

http://www.btechsmartclass.com/data_structures/tree-terminology.html

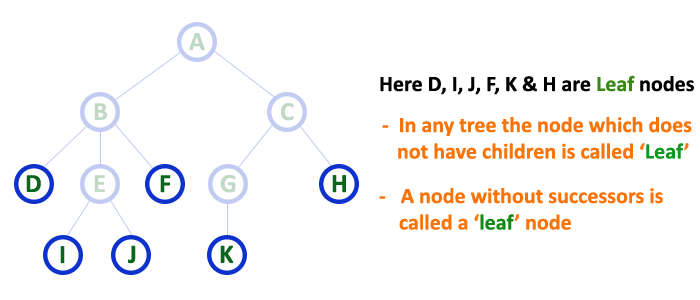
  - 트리의 깊이 : 루트에서 리프까지의 경로의 길이, Depth

http://www.btechsmartclass.com/data_structures/tree-terminology.html

  - 트리의 특성
    ① 루트는 하나
    ② 방향성 존재
    ③ 순환 구조가 없음
  - 이진 트리 : 모든 노드가 최대 2개(0~2)의 자식 노드를 가지는 트리

http://www.btechsmartclass.com/data_structures/binary-tree.html

  - 완전 이진 트리 : Complete binary tree 또는 Perfect Binary Tree. 마지막 레벨을 제외하고 모든 노드가 채워져 있고, 마지막 레벨 노드가 왼쪽부터 채워져 있음

http://www.btechsmartclass.com/data_structures/binary-tree.html

  - 포화 이진 트리 : 모든 레벨에서 모든 노드들이 채워져 있음.

http://www.btechsmartclass.com/data_structures/binary-tree.html

  - 이진 탐색 트리 : Binary Search Tree. 모든 부모 노드의 값이 왼쪽 자식 트리에 있는 값보다는 크고 오른쪽 자식 트리에 있는 값보다는 작은 형태의 트리

http://www.btechsmartclass.com/data_structures/binary-search-tree.html

  - 트리 관련 문제의 핵심은 탐색 (루트 노드가 주어졌을 때 트리를 구석구석 훑어가며 원하는 목적을 달성하는 것)

4. 너비 우선 탐색
  - 너비 우선 탐색 : Breadth First Search. 반복(while, for 등) 기반의 탐색. 큐에 노드를 순서대로 넣고 빼는 방식으로 탐색
  - 이진 트리 출력하기

import queue

class Node():
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

def listToCompleteBinaryTree(lst):
    def helper(index):
        if index >= len(lst):
            return None
        node = Node(lst[index])
        node.left = helper(index * 2 + 1)
        node.right = helper(index * 2 + 2)
        return node
    return helper(0)

def printTree(node):
    all_lines = []
    line = []
    
    q = queue.Queue()
    q.put(node)
    q.put(Node(-1)) # -1 통해서 각 깊이를 구별
    
    while q.qsize() > 0:
        node = q.get() # 임시 노드를 큐에 가장 먼저 들어와 있던 걸 빼냄
        
        if not node:
            continue
        else:
            if node.val == -1:  # -1 만나면 새 리스트 만듦
                if q.qsize() > 0:
                    all_lines.append(line)
                    line = []
                    q.put(Node(-1))
                    
            else :
                line.append(node.val)
                q.put(node.left)
                q.put(node.right)

    return all_lines

5. 깊이 우선 탐색
  - 깊이 우선 탐색 : Depth First Search. 재귀 기반의 탐색. 가장 깊은 곳까지 내려갔다가 오는 방식의 탐색.
  - 트리의 경로의 합

class Node():
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

def listToCompleteBinaryTree(lst):
    def helper(index):
        if index >= len(lst):
            return None
        node = Node(lst[index])
        node.left = helper(index * 2 + 1)
        node.right = helper(index * 2 + 2)
        return node
    return helper(0)

def printTree(node):
    q = [Node(-1), node]

    line = []
    while q:
        node = q.pop()
        if not node:
            continue
        elif node.val == -1:
            if len(line) > 0:
                print(" ".join(line))
                line = []
                q.insert(0,Node(-1))
        else:
            q.insert(0,node.left)
            q.insert(0,node.right)
            line.append(str(node.val))

def path_sum(node, targetSum):
    def dfsHelper(node, curSum):
        if node is None: # 리프 노드일 때 합계가 목표와 같은지 체크
            if curSum == targetSum:
                return True
            else:
                return False
        else:
            curSum += node.val
            is_left = dfsHelper(node.left, curSum)
            is_right = dfsHelper(node.right, curSum)
        
        
        return is_left or is_right
    
    dfsHelper(node, 0)
    return dfsHelper(node, 0)

---

전쟁같던 개인 프로젝트가 끝나고 CS의 꽃인 자료구조와 알고리즘이 나왔다...ㅎ
플젝만 끝나면 살 것 같았는데.... 🤦‍♀️🤦‍♀️🤦‍♀️

※ 수업 자료의 출처는 K-Digital Training x 엘리스 인공지능 서비스 개발 기획 1기 (elice.io/)입니다.